নবম ও দশম শ্রেণীর অংক সমাধান ২০২৪-২৫ (অধ্যায়ঃ১৬.৪ ঘনবস্তুর ক্ষেত্র)

ঘনবস্তুর ক্ষেত্র:

১. একটি সামন্তরিকের দুইটি সন্নিহিত বাহুর দৈর্ঘ্য যথাক্রমে ৭ সেমি এবং ৫ সেমি। এর পরিসীমার অর্ধেক কত সেমি?
ক) ১২
খ) ২০
গ) ২৪
ঘ) ২৮

উত্তর: ক

ব্যাখ্যাঃ

সামন্তরিকের পরিসীমা নির্ণয় করা হয় এর চারটি বাহুর যোগফল দিয়ে।

সামন্তরিকের দুইটি সন্নিহিত বাহুর দৈর্ঘ্য দেওয়া আছে:
7 সেমি এবং 5 সেমি।

সামন্তরিকের পরিসীমা হবে:
2 × (7 + 5) = 2 × 12 = 24 সেমি।

পরিসীমার অর্ধেক:
24 ÷ 2 = 12 সেমি।

২. একটি সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য ৬ সেমি। এর ক্ষেত্রফল কত বর্গ সেমি?
ক) 333\sqrt{3}33​
খ) 434\sqrt{3}43​
গ) 636\sqrt{3}63​
ঘ) 939\sqrt{3}93​

উত্তর: ঘ

ব্যাখ্যাঃ

একটি সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য ৬ সেমি হলে তার ক্ষেত্রফল নির্ণয়ের সূত্র হলো:

ক্ষেত্রফল = (√3 / 4) * (বাহুর দৈর্ঘ্য)²

এখানে, বাহুর দৈর্ঘ্য = ৬ সেমি

সুতরাং, ক্ষেত্রফল = (√3 / 4) * (৬)² = (√3 / 4) * ৩৬ = ৯√3 বর্গ সেমি

√3 এর মান প্রায় ১.৭৩২। তাই, ক্ষেত্রফল প্রায় ৯ * ১.৭৩২ = ১৫.৫৮৮ বর্গ সেমি।

উত্তরঃ সমবাহু ত্রিভুজটির ক্ষেত্রফল ৯√3 বর্গ সেমি অথবা প্রায় ১৫.৫৮৮ বর্গ সেমি।

৩. সমতল জ্যামিতির নিচের তথ্যগুলো বিশ্লেষণ করো:
(i) সমবাহু ত্রিভুজের প্রতিটি কোণ এক সমকোণের চেয়ে ছোট।
(ii) সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের সমষ্টি এক সমকোণের সমান।
(iii) ত্রিভুজের কোনো বাহু বর্ধিত করলে উৎপন্ন বহিস্থ কোণ বিপরীত অভ্যন্তরীণ কোণদ্বয়ের সমষ্টির চেয়ে বড়।

নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii

উত্তর: ঘ

৪. একটি বর্গক্ষেত্রে প্রতি বাহুর দৈর্ঘ্য $a$ এবং কর্ণ $d$।
(i) ক্ষেত্রফল a2a^2a2 বর্গ একক।
(ii) পরিসীমা $2ad$ একক।
(iii) d=2ad = \sqrt{2}ad=2​a।

নিচের কোনটি সঠিক?
ক) i ও ii
খ) i ও iii
গ) ii ও iii
ঘ) i, ii ও iii

উত্তর: খ

৫-৭ নম্বর প্রশ্নের জন্য চিত্র দেখে উত্তর দাও।

৫. ABCD আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য কত সেমি?
ক) ১৩
খ) ১৪
গ) ১৪.৪
ঘ) ১৫

উত্তর: গ

৬. ADF ত্রিভুজের ক্ষেত্রফল কত বর্গ সেমি?
ক) ১৬
খ) ৩২
গ) ৬৪
ঘ) ১২৮

উত্তর: যথাযথ তথ্য না থাকায় প্রশ্নের উত্তর সম্ভব নয়।

৭. AGB অর্ধবৃত্তের ক্ষেত্রফল কত বর্গ সেমি?
ক) ১৮
খ) $\mathrm{১৮}.\mathrm{৮৫}$ (প্রায়)
গ) $\mathrm{৩৭}.\mathrm{৭}$ (প্রায়)
ঘ) ৯৬

উত্তর: খ

৮. একটি আয়তাকার ঘনবস্তুর দৈর্ঘ্য ১৬ মিটার, প্রস্থ ১২ মিটার এবং উচ্চতা ৪.৫ মিটার। এর পৃষ্ঠতলের ক্ষেত্রফল, কর্ণের দৈর্ঘ্য এবং আয়তন নির্ণয় কর।

সমাধান:

পৃষ্ঠতলের ক্ষেত্রফল:

=2(ab+ca+bc)

=2(16✕12+4.5✕16+12✕4.5)

=2(192+72+54)

=2✕318

=636 বর্গ মিটার

আয়তাকার ঘনবস্তুর কর্ণের দৈর্ঘ্য

=√(a²+b²+c²)

=√{(16)²+(12)²+(4.5)²}

=√(256+144+20.25)

=√420.25

=20.5 মিটার

আয়তাকার ঘনবস্তুর আয়তন

=a✕b✕c

=16✕12✕4.5

864 ঘন একক।

বিকল্প পদ্ধতিঃ

৯. একটি আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত 21 : 16 : 12 এবং কর্ণের দৈর্ঘ্য 87 সেমি হলে, ঘনবস্তুটির তলের ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

ধরি, আয়তাকার ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে a, b ও c.

মনে করি, a=21x, b=16x, x=12x

∴কর্ণের দৈর্ঘ্য

=√(a²+b²+c²)

=√{(21x)²+(16x)²+(12x)²}

 =√(441x²+256x²+144x²)

=√(841x²)

প্রশ্নমতে,

√(841x²)=87

বা,  {√(841x²}²=(87)²

বা,  841x²=7569

বা,  x²=7569/841

বা,  x²=9

বা,  x=√9

বা,  x=3

∴ a=21✕3=63, b=16✕3=48, x=12✕3=36

∴ আয়তাকার ঘনবস্তুর তলের ক্ষেত্রফল

=2(ab+ca+bc)

=2(63✕48+36✕63+48✕36)

=2(3024+2268+1728)

=2✕7020

=14040 বর্গ সেমি।

বিকল্প পদ্ধতিঃ

১০. একটি আয়তাকার ঘনবস্তু 48 বর্গমিটার ভূমির উপর দন্ডায়মান। এর উচ্চতা 3 মিটার এবং কর্ণ 13 মিটার। আয়তাকার ঘনবস্তুর দৈর্ঘ্য ও প্রস্থ নির্ণয় কর।

সমাধানঃ

মনে করি, আয়তাকার ঘনবস্তুর দৈর্ঘ্য = a মি.

এবং আয়তাকার ঘনবস্তুর প্রস্থ = b মি.

∴ভূমির ক্ষেত্রফল ab= বর্গ মি =48 বর্গ মি

আয়তাকার ঘনবস্তুর উচ্চতা c=3 মি হলে,

13=√(a²+b²+c²)

বা,  169=a²+b²+c²

বা,  169=a²+b²+3²

বা,  169=a²+b²+9

বা,  a²+b²=169-9

বা,  a²+b²=160

বা,  (a+b)²-2ab=160

বা,  (a+b)²=160+2ab

বা,  (a+b)²=160+2✕48 [ab=48]

বা,  (a+b)²=256

বা,  a+b=16…………(i)

আবার,

a²+b²=160

বা,  (a-b)²+2ab=160

বা,  (a-b)²=160-2ab

বা,  (a-b)²=160-2✕48

বা,  (a-b)²=64

বা,  a-b=8……………(ii)

(i)+(ii) করে পাই,

2a=24

বা,  a=24/2

বা,  a=12

(i)-(ii) করে পাই,

2b=8

বা,  b=8/2

বা,  b=4

∴আয়তাকার ঘনবস্তুর দৈর্ঘ্য=12 মিটার ও প্রস্থ=4 মিটার।

বিকল্প পদ্ধতিঃ

১১. একটি আয়তাকার কাঠের বাক্সের বাইরের মাপ যথাক্রমে 8 সেমি, 6 সেমি ও 4 সেমি। এর ভিতরের সম্পূর্ণ পৃষ্ঠের ক্ষেত্রফল 88 বর্গ সেমি। বাক্সটির কাঠের পুরুত্ব নির্ণয় কর।

সমাধানঃ

মনে করি, কাঠের পুরুত্ব= x সেমি

∴ বাক্সের ভেতরের দৈর্ঘ্য a=(8-2x) সেমি

বাক্সের ভিতরের প্রস্থ b=(6-2x) সেমি

এবং বাক্সের ভিতরের উচ্চতা c=(4-2x) সেমি

∴ বাক্সের ভিতরের সমগ্র পৃষ্টের ক্ষেত্রফল

=2(ab+bc+ca)

=2{(8-2x)(6-2x)+(6-2x)(4-2x)+(4-2x)(8-2x)}

=2(48-12x-16x+4x²+24-8x-12x+4x²+32-16x-8x+4x²)

=2(12x²-72x+104)

প্রশ্নমতে,

2(12x²-72x+104)=88

বা,  12x²-72x+104=44

বা,  12x²-72x+104-44=0

বা,  12x²-72x+60=0

বা,  12(x²-6x+5)=0

বা,  x²-6x+5=0

বা,  x²-5x-x+5=0

বা,  x(x-5)-1(x-5)=0

বা,  (x-1)(x-5)=0

বা,  x-1=0        অথবা, x-5=0

বা,  x=1            বা,  x=5

যেহেতু বাক্সের বাইরের উচ্চতা 4 সেমি সেহেতু ভেতরের উচ্চতা 5 সেমি হতে পারে না।

∴ বাক্সের পুরুত্ব 1 সেমি।

বিকল্প পদ্ধতিঃ

১২. একটি দেওয়ালের দৈর্ঘ্য 25 মিটার, উচ্চতা 6 মিটার এবং পুরুত্ব 30 সেমি। একটি ইটের দৈর্ঘ্য 10 সেমি, প্রস্থ 5 সেমি এবং উচ্চতা 3 সেমি। দেয়ালটি ইট দিয়ে তৈরি করতে প্র্যোজনীয় ইটের সংখ্যা নির্ণয় কর।

সমাধানঃ

দেওয়া আছে,

দেওয়ালের দৈর্ঘ্য=২৫ মিটার=২৫০০ সেমি

প্রস্থ=৬ মিটার=৬০০ সেমি

পুরুত্ব=৩০ সেমি

∴দেওয়ালটির আয়তন

=দৈর্ঘ্য✕প্রস্থ✕পুরুত্ব

=(২৫০০✕৬০০✕৩০) ঘন সেমি

=৪,৫০,০০,০০০ ঘন সেমি

আবার, একটি ইটের দৈর্ঘ্য=১০ সেমি

প্রস্থ=৫ সেমি

পুরুত্ব বা উচ্চতা =৩ সেমি

ইটের আয়তন

=১০✕৫✕৩ ঘন সেমি

=১৫০ ঘন সেমি

∴দেওয়ালটি তৈরিতে ইট প্রয়োজন

   ৪,৫০,০০,০০০

=———–

      ১৫০

উত্তরঃ ৩,০০,০০০ টি

বিকল্প পদ্ধতিঃ

দেয়ালের দৈর্ঘ্য ২৫ মিটার, উচ্চতা ৬ মিটার এবং পুরুত্ব ৩০ সেমি। ইটের দৈর্ঘ্য ১০ সেমি, প্রস্থ ৫ সেমি এবং উচ্চতা ৩ সেমি। দেয়ালটি তৈরি করতে প্রয়োজনীয় ইটের সংখ্যা বের করতে হলে প্রথমে দেয়ালের আয়তন এবং একটি ইটের আয়তন বের করতে হবে। তারপর দেয়ালের আয়তনকে ইটের আয়তন দিয়ে ভাগ করলেই প্রয়োজনীয় ইটের সংখ্যা পাওয়া যাবে।

১. দেয়ালের আয়তন:

দেয়ালের পরিমাপগুলো একই এককে নিতে হবে। আমরা সেমি এককে পরিবর্তন করব:

• দৈর্ঘ্য = ২৫ মিটার = ২৫ × ১০০ = ২৫০০ সেমি
• উচ্চতা = ৬ মিটার = ৬ × ১০০ = ৬০০ সেমি
• পুরুত্ব = ৩০ সেমি

দেয়ালের আয়তন = দৈর্ঘ্য × উচ্চতা × পুরুত্ব = ২৫০০ × ৬০০ × ৩০ = ৪৫,০০,০০০ ঘন সেমি

২. একটি ইটের আয়তন:

• দৈর্ঘ্য = ১০ সেমি
• প্রস্থ = ৫ সেমি
• উচ্চতা = ৩ সেমি

ইটের আয়তন = ১০ × ৫ × ৩ = ১৫০ ঘন সেমি

৩. প্রয়োজনীয় ইটের সংখ্যা:

প্রয়োজনীয় ইটের সংখ্যা = দেয়ালের আয়তন / একটি ইটের আয়তন = ৪৫,০০,০০০ / ১৫০ = ৩,০০,০০০ টি

অতএব, দেয়ালটি তৈরি করতে ৩০০,০০০ টি ইটের প্রয়োজন।

১৩. একটি ঘনক আকৃতির বস্তুর পৃষ্টতলের ক্ষেত্রফল  2400 বর্গ সেমি হলে, এর কর্ণের দৈর্ঘ্য কত?

সমাধানঃ

আমরা জানি,

ঘনকের দৈর্ঘ্য=প্রস্থ=উচ্চতা

ধরি, দৈর্ঘ্য=প্রস্থ=উচ্চতা=a

∴ ঘনক আকৃতির বস্তুর পৃষ্টতলের ক্ষেত্রফল

=2(a²+a²+b²)

=2.3a²

=6a²

প্রশ্নমতে,

6a²=2400

বা,  a²=2400/6

বা,  a²=400

বা,  a=√400

বা,  a=20

∴ঘনক আকৃতির বস্তুর কর্ণ

=√(a²+a²+a²)

=√(3a²)

=√(3.20²)

=√(3.400)

=√1200

উত্তর: 34.641 সেমি (প্রায়)

বিকল্প পদ্ধতিঃ

একটি ঘনক আকৃতির বস্তুর পৃষ্ঠতলের ক্ষেত্রফল ২৪০০ বর্গ সেমি হলে, এর কর্ণের দৈর্ঘ্য নির্ণয় করার জন্য প্রথমে ঘনকের একটি বাহুর দৈর্ঘ্য বের করতে হবে।

আমরা জানি, ঘনকের ৬টি তল থাকে এবং প্রতিটি তল বর্গাকার। যদি একটি বাহুর দৈর্ঘ্য ‘a’ হয়, তাহলে পৃষ্ঠতলের ক্ষেত্রফল হবে ৬a²।

প্রশ্নমতে, ৬a² = ২৪০০

অতএব, a² = ২৪০০ / ৬ = ৪০০

সুতরাং, a = √৪০০ = ২০ সেমি

এখন, ঘনকের কর্ণের দৈর্ঘ্য নির্ণয়ের সূত্র হলো a√3, যেখানে a হলো বাহুর দৈর্ঘ্য।

অতএব, কর্ণের দৈর্ঘ্য = ২০√3 সেমি

√3 এর আসন্ন মান ১.৭৩২। তাই,

কর্ণের দৈর্ঘ্য = ২০ × ১.৭৩২ ≈ ৩৪.৬৪ সেমি (প্রায়)

উত্তরঃ ঘনক আকৃতির বস্তুটির কর্ণের দৈর্ঘ্য ২০√3 সেমি অথবা প্রায় ৩৪.৬৪ সেমি।

১৪. ১২ সেমি উচ্চতাবিশিষ্ট একটি বেলনের ভূমির ব্যাসার্ধ ৫ সেমি। এর পৃষ্টতলের ক্ষেত্রফল ও আয়তন নির্ণয় কর।

সমাধানঃ

মনে করি,

বেলনের ভূমির ব্যাসার্ধ r= 5 সেমি

এবং উচ্চতা h=12 সেমি

তাহলে, বেলনের সম্পুর্ণ পৃষ্ঠের ক্ষেত্রফল

=2 π r(h+r)

=2✕3.1416✕5✕(12+5)

=2✕3.1416✕5✕17

=534.072 বর্গ সেমি।

এবং বেলনের আয়তন

= πr²h

=3.1416✕(5)²✕12

=3.1416✕25✕12

উত্তর: 942.48 ঘন সেমি

বিকল্প পদ্ধতিঃ 

১৫. একটি বেলনের বক্রতলের ক্ষেত্রফল 100 বর্গসেমি এবং আয়তন 150 ঘন সেমি। বেলনের উচ্চতা এবং ব্যাসার্ধ নির্ণয় কর।

সমাধানঃ

মনে করি বেলনের ভূমির ব্যাসার্ধ r সেমি এবং উচ্চতা h সেমি

তাহলে,

বেলনের বক্রতলের ক্ষেত্রফল = 2πrh বর্গ সেমি

এবং বেলনের আয়তন = πr²h ঘন সেমি

প্রশ্নমতে,

πr²h=150……….(i)

এবং

2πrh=100

বা,   πrh=50……….(ii)

(i) ÷(ii) করে পাই,

r=3

 (ii) নং এ r এর মান বসিয়ে পাই,

π✕3✕h=50

বা,  3.1416✕3✕h=50

বা,  9.4248✕h=50

বা,  h=50/9.4248

বা,  h=5.3052 সেমি।

উত্তর:

∴ বেলনের ব্যাসার্ধ = 3 সেমি

এবং  বেলনের উচ্চতা = 5.3052 সেমি

বিকল্প পদ্ধতিঃ 

১৬. একটি সমবৃত্তভূমিক সিলিন্ডারের ক্ষেত্রফল 4400 বর্গ সেমি। এর উচ্চতা 30 সেমি হলে সমগ্রতলের ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

আমরা জানি,

সমবৃত্তভূমিক সিলিন্ডারের বক্রতলের ক্ষেত্রফল =2πrh; এখানে h=30=সমবৃত্তভূমিক সিলিন্ডারের উচ্চতা ও r=ভুমির ব্যাসার্ধ।

প্রশ্নমতে,

2πrh=4400

বা,  2✕3.1416✕r✕30=4400

বা,  r✕188.496=4400

বা,  r=4400/188.496

বা,  r=23.3427 সেমি

আবার, সিলিন্ডারের সমগ্রতলের ক্ষেত্রফল

=2πr(r+h)

=2✕3.1416✕23.3427(23.3427+30)

=2✕3.1416✕23.3427✕53.3427

=7823.6059 বর্গ সেমি।

 ∴উত্তর: সিলিন্ডারের সমগ্রতলের ক্ষেত্রফল 7823.6059 বর্গ সেমি।

বিকল্প পদ্ধতিঃ 

১৭. একটি লোহার পাইপের ভিতরের ও বাইরের ব্যাস যথাক্রমে 12 সেমি ও 14 সেমি এবং পাইপের উচ্চতা 5 মিটার। এক ঘন সেমি লোহার ওজন 7.2 গ্রাম হলে পাইপের লোহার ওজন নির্ণয় কর।

সমাধানঃ

দেওয়া আছে,

পাইপের উচ্চতা h=5 মিটার=500 সেমি

পাইপের বাইরের ব্যাস=14 সেমি

পাইপের বাইরের ব্যাসার্ধ r₁=14/2 সেমি=7 সেমি

∴ পাইপের বাইরের আয়তন

=πr₁²h

=3.1416✕(7)²✕500

=76969.2 ঘন সেমি

আবার, পাইপের ভিতরের ব্যাস=12 সেমি

পাইপের ভিতরের ব্যাসার্ধ r₂=12/2 সেমি=6 সেমি

∴ পাইপের ভিতরের আয়তন

=πr₂²h

=3.1416✕(6)²✕500

=56548.8 ঘন সেমি

∴ লোহার আয়তন

=76969.2 ঘন সেমি-56548.8 ঘন সেমি

=20420.4 ঘন সেমি।

এখন,

1 ঘন সেমি লোহার ওজন 7.2 গ্রাম

∴20420.4 ঘন সেমি লোহার ওজন =20420.4✕7.2 গ্রাম

=147026.88 গ্রাম

=147.02688 কিলোগ্রাম

∴উত্তর:  পাইপের লোহার ওজন=147.02688 কিলোগ্রাম

বিকল্প নিয়মঃ 

১৮. একটি আয়তাকারক্ষেত্রের দৈর্ঘ্য12 মিটার এবং প্রস্থ 5 মিটার। আয়তাকারক্ষেত্রটিকে পরিবেষ্টিত করে একটি বৃত্তাকারক্ষেত্র আছে যেখানে আয়তাকারক্ষেত্র দ্বারা আনধিকৃত অংশে ঘাস লাগানো হলো।

ক) উপরের তথ্যের ভিত্তিতে সংক্ষিপ্ত বর্ণনাসহ চিত্র আঁক।

সমাধানঃ

মনে করি, ABCD একটি আয়তক্ষেত্র যার দৈর্ঘ্য 12 মিটার ও প্রস্থ 5 মিটার। এই আয়তক্ষেত্রটিকে পরিবেষ্টিত করে একটি বৃত্তাকার ক্ষেত্র আছে যার কেন্দ্র O. ABCD আয়তক্ষেত্রের কর্ণ হবে বৃত্তের ব্যাস। নির্ণেয় চিত্রটি হলোঃ

খ) বৃত্তাকার ক্ষেত্রটির ব্যাস নির্ণয় কর।

সমাধানঃ

ক এর বর্ণনা অনুসারে বৃত্তটির ব্যাস হলো বৃত্তে অন্তর্লিখিত আয়তক্ষেত্রের কর্ণ।

∴আয়তক্ষেত্রের কর্ণ

=√(দৈর্ঘ্য^২+প্রস্থ^২)

=√(12²+5²)

=√(144+25)

=√169

=13 মিটার।

∴উত্তর: বৃত্তটির ব্যাস 13 মিটার।

গ) প্রতি বর্গমিটার ঘাস লাগাতে 50 টাকা খরচ হলে মোট খরচ নির্ণয় কর।

সমাধানঃ

বৃত্তটির ব্যাস=13 মিটার

∴বৃত্তের ব্যাসার্ধ r=13/2 মিটার=6.5 মিটার

∴বৃত্তের ক্ষেত্রফল

= πr²

=3.1416✕(6.5)²

=132.7326 বর্গ মি।

আবার,

আয়তক্ষেত্রের ক্ষেত্রফল

=দৈর্ঘ্য✕প্রস্থ

=12✕5

=60 বর্গ মিটার

∴ বৃত্তের অনাধিকৃত অংশের পরিমাণ

=132.7326-60

=72.7326 বর্গ মি

এখন,

1 বর্গ মিটার ঘাস লাগাতে খরচ হয় 50 টাকা

∴ 72.7326 বর্গ মিটার ঘাস লাগাতে খরচ হয় =72.7326✕50 টাকা

                                                            =3636.63 টাকা

∴উত্তর: মোট খরচ 3636.63 টাকা।

১৯. চিত্রটি বর্গক্ষেত্র ও বর্গকলায় বিভক্ত।

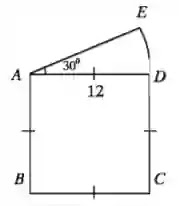
ক) বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য ও পরিসীমা নির্ণয় কর।

সমাধানঃ

দেওয়া আছে, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a=12 cm

∴বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য

=√2a

=√2✕12

=16.971 cm

এবং বর্গক্ষেত্রের পরিসীমা

=4a

=4✕12

=48 cm

খ) সম্পূর্ণ ক্ষেত্রের ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

দেওয়া আছে,

বৃত্তাংশের ব্যাসার্ধ r=AD=AE=12 cm

কেন্দ্রে উৎপন্ন কোণ θ=30⁰

∴ADE বৃত্তাংশের ক্ষেত্রফল

    θ

=——✕ πr²

    360⁰

   30⁰

=——✕ π(12)²

    360⁰

=37.6992 বর্গ সেমি

এবং বর্গক্ষেত্রের ক্ষেত্রফল

=(AB)²

=(12)²

=144 বর্গ সেমি

∴ সম্পূর্ণ ক্ষেত্রের ক্ষেত্রফল

=37.6992 বর্গ সেমি+144 বর্গ সেমি

উত্তর: 181.699 বর্গ সেমি।

গ) বর্গের বাহুর দৈর্ঘ্যবিশিষ্ট কোনো সুষম ষড়ভূজ কোনো বৃত্তে অন্তর্লিখিত হলে বৃত্তের অনধিকৃত অংশের ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

মনে করি,

সুষম ষড়ভুজের বাহুর দৈর্ঘ্য, r=12 সেমি

এবং সুষম ষড়ভূজের বাহুর সংখ্যা, n=6

যদি বাহুর দৈর্ঘ্য ১২ মিটার হয়, তাহলে বৃত্তের ব্যাসার্ধও ১২ মিটার হবে। কারণ, সুষম ষড়ভুজের কেন্দ্র থেকে প্রতিটি শীর্ষের দূরত্ব বাহুর দৈর্ঘ্যের সমান।

এখন,

• বৃত্তের ক্ষেত্রফল = πr² = π × ১২² = ১৪৪π বর্গ মিটার
• সুষম ষড়ভুজের ক্ষেত্রফল = (3√3/2)a² = (3√3/2) × ১২² = (3√3/2) × ১৪৪ = ২১৬√3 বর্গ মিটার

বৃত্তের অনধিকৃত অংশের ক্ষেত্রফল = বৃত্তের ক্ষেত্রফল – সুষম ষড়ভুজের ক্ষেত্রফল

= ১৪৪π – ২১৬√3

π এর মান ৩.১৪১৬ এবং √3 এর মান ১.৭৩২ বসালে,

= ১৪৪ × ৩.১৪১৬ – ২১৬ × ১.৭৩২

= ৪৫২.৩৯ – ৩৭৪.১২

= ৭৮.২৭ বর্গ মিটার (প্রায়)

অতএব, বৃত্তের অনধিকৃত অংশের ক্ষেত্রফল প্রায় ৭৮.২৭ বর্গ মিটার।

সংক্ষেপে:

যদি সুষম ষড়ভুজের বাহুর দৈর্ঘ্য ‘a’ হয়, তাহলে:

• বৃত্তের ব্যাসার্ধ = a
• বৃত্তের ক্ষেত্রফল = πa²
• সুষম ষড়ভুজের ক্ষেত্রফল = (3√3/2)a²
• বৃত্তের অনধিকৃত অংশের ক্ষেত্রফল = a²(π – (3√3/2)) ≈ 0.5436a²

এই ক্ষেত্রে, a = ১২ মিটার।

অতএব, বৃত্তের অনধিকৃত অংশের ক্ষেত্রফল = ১২²(π – (3√3/2)) ≈ 0.5436 × ১২² = 0.5436 × ১৪৪ ≈ ৭৮.২৭ বর্গ মিটার।

২০. একটি সামন্তরিকক্ষেত্র ABCD এবং একটি আয়তক্ষেত্র BCEF উভয়ের ভূমি BC.

ক) একি উচ্চতা বিবেচনা করে সামন্তরিক ও আয়তক্ষেত্রটির চিত্র আঁক।

সমাধানঃ

একই ভূমি BC এর উপর ABCD একটি সামন্তরিক ক্ষেত্র ও BCEF একটি আয়তক্ষেত্র যাদের উচ্চতা AM.

খ) দেখাও যে, ABCD ক্ষেত্রটির পরিসীমা BCEF ক্ষেত্রটির পরিসীমা অপেক্ষা বৃহত্তর।

সমাধানঃ

ABCD ক্ষেত্রটির পরিসীমা

=AB+BC+CD+AD

=AB+BC+AB+BC [সামন্তরিকের বিপরীত বাহু সমান হয়]

=2AB+2BC………(i)

BCEF ক্ষেত্রটির পরিসীমা

=FB+BC+CE+EF

=FB+BC+FB+BC [আয়তক্ষেত্রের বিপরীত বাহু সমান হয়]

=2FB+2BC……….(ii)

এখন,

△ABF এ ∠BFA=90⁰

∴ AB> BF [সমকোণী ত্রিভুজে অতিভুজ বৃহত্তম বাহু]

তাহলে, AB> BF হলে, (i) ও (ii) তুলনা করে পাই,

2FB+2BC>2FB+2BC

বা, ABCD ক্ষেত্রটির পরিসীমা> BCEF ক্ষেত্রটির পরিসীমা

∴ABCD ক্ষেত্রটির পরিসীমা BCEF ক্ষেত্রটির পরিসীমা অপেক্ষা বৃহত্তর (দেখানো হলো)

গ) আয়তক্ষেত্রটির দৈর্ঘ্য ও প্রস্থের অনুপাত 5 : 3 এবং ক্ষেত্রটির পরিসীমা 48 মিটার হলে, সামন্তরিকটির ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

মনে করি, আয়তক্ষেত্রটির দৈর্ঘ্য=5x মিটার এবং প্রস্থ=3x মিটার

∴2(5x+3x)=48

বা, 2✕8x=48

বা, 16x=48

বা, x=48/16

বা, x=3

আয়তক্ষেত্রটির দৈর্ঘ্য=5✕3=15 মিটার এবং প্রস্থ=3✕3=9 মিটার।

এখন,

আয়তক্ষেত্রের দৈর্ঘ্য=সামন্তরিকের ভুমি=15 মিটার

এবং আয়তক্ষেত্রের প্রস্থ= সামন্তরিকের উচ্চতা =9 মিটার

∴ সামন্তরিকের ক্ষেত্রফল

=ভুমি✕উচ্চতা

=15✕9

উত্তর: 135 বর্গ মিটার

২১. একটি বর্গক্ষেত্রের পরিসীমা একটি আয়তক্ষেতের পরিসীমার সমান। আয়তক্ষেত্রটির দৈর্ঘ্য প্রস্থের তিনগুণ এবং ক্ষেত্রফল 1200 বর্গমিটার।

ক) x চলকের মাধ্যমে আয়তক্ষেত্রের পরিসীমা নির্ণয় কর।

সমাধানঃ

ছবি

মনে করি,

আয়তক্ষেত্রের প্রস্থ=x মিটার

∴আয়তক্ষেত্রের দৈর্ঘ্য=3x মিটার

∴আয়তক্ষেত্রের পরিসীমা=2(x+3x)=2✕4x=8x মিটার।

খ) বর্গক্ষেত্রটির ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

আয়তক্ষেত্রের ক্ষেত্রফল=x✕3x বর্গ মি=3x² বর্গ মি

প্রশ্নমতে,

3x²=1200

বা, x²=1200/3

বা, x²=400

বা, x=√400

বা, x=20

∴আয়তক্ষেত্রের পরিসীমা=2(20+3✕20)=2✕4✕20=160 মিটার।

শর্তমতে,

আয়তক্ষেত্রের পরিসীমা=বর্গক্ষেত্রের পরিসীমা

∴ বর্গের বাহুর দৈর্ঘ্য, a=160/4=40 মিটার।

অতএব,

বর্গক্ষেত্রের ক্ষেত্রফল

=a²

=(40)²

উত্তর: 1600 বর্গ মি

গ) আয়তক্ষেত্রের বাইরে চতুর্দিকে 1.5 মিটার চওড়া একটি রাস্তা তৈরি করতে 25✕12.5 বর্গসেমি তলবিশিষ্ট ইটের সংখ্যা নির্ণয় কর।

সমাধানঃ

আয়তক্ষেত্রের দৈর্ঘ্য=3x=3✕20=60 মিটার এবং প্রস্থ=20 মিটার

∴ আয়তক্ষেত্রের ক্ষেত্রফল = 60✕20 বর্গ মি =1200 বর্গ মি

রাস্তাসহ আয়তক্ষেত্রের দৈর্ঘ্য=60+2✕1.5 মি=63 মি

রাস্তাসহ আয়তক্ষেত্রের প্রস্থ=20+2✕1.5 মি=23  মি

∴রাস্তাসহ আয়তক্ষেত্রের ক্ষেত্রফল=63✕23 বর্গ মি=1449 বর্গ মি.

তাহলে,

রাস্তার ক্ষেত্রফল=1449 বর্গ মি-1200 বর্গ মি=249 বর্গ মি

ইটের তলার ক্ষেত্রফল

=25✕12.5 বর্গসেমি

=25✕12.5÷ 100✕100

=0.03125 বর্গসেমি

∴ইটের সংখ্য্যা

249÷ 0.03125 = 7968  টি

উত্তর: ইটের সংখ্যা 7968 টি