জ্যামিতিক প্রতিসমতা ও প্রতিসাম্যঃ
১. সমতলীয় জ্যামিতির ক্ষেত্রে –
(i) ত্রিভুজ হলো ন্যূনতম সংখ্যক রেখাংশ দ্বারা গঠিত একটি বহুভুজ।
(ii) চারটি সমান বাহুবিশিষ্ট যেকোনো চিত্রই রম্বস।
(iii) একটি সুষম পঞ্চভুজের প্রতিটি বাহুর দৈর্ঘ্য সমান হলেও এর কোণগুলির মান ভিন্ন ভিন্ন হয়ে থাকে।
নিচের বিকল্পগুলির মধ্যে কোনটি/কোনগুলি নির্ভুল?
ক) শুধুমাত্র (i)
খ) (i) এবং (ii) উভয়ই
গ) (i) এবং (iii) উভয়ই
ঘ) (i), (ii) এবং (iii) প্রত্যেকটি
উত্তরঃ ক
২. একটি বিষমবাহু ত্রিভুজের মধ্যে কয়টি প্রতিসাম্য রেখা বিদ্যমান?
ক) একটিও নয়
খ) কেবল একটি
গ) মোট তিনটি
ঘ) অসংখ্য
উত্তরঃ ক
আপনার জন্য- নবম ও দশম শ্রেণীর অংক সমাধান ২০২৪-২৫ (অধ্যায়ঃ ১৫ ক্ষেত্রফল সম্পর্কিত সমস্যা)
চিত্র হতে ৩ ও ৪ নং প্রশ্নের উত্তর দাও। বহুভুজটির প্রতিটি বাহুর দৈর্ঘ্য 6 সেমি।

৩. বহুভুজটির মোট কতগুলি প্রতিসাম্য রেখা?
ক) ৩টি
খ) ৬টি
গ) ৭টি
ঘ) অসংখ্য
উত্তরঃ খ
৪. বহুভুজটির ক্ষেত্রে –
(i) ঘূর্ণন মাত্রা ৪
(ii) ঘূর্ণন কোণ ৬০°
(iii) প্রতিটি কোণ সমান
নিম্নলিখিত বিকল্পগুলির মধ্যে কোনটি/কোনগুলি সঠিক?
ক) শুধুমাত্র (i)
খ) শুধুমাত্র (ii)
গ) (ii) এবং (iii) উভয়ই
ঘ) (i), (ii) এবং (iii) প্রত্যেকটি
উত্তরঃ গ
৫. নিম্নলিখিত চিত্রগুলির মধ্যে কোনটিতে প্রতিসাম্য রেখা বিদ্যমান?
ক) একটি সাধারণ বাড়ির চিত্র সমাধান: সাধারণভাবে, একটি সাধারণ বাড়ির চিত্রে প্রতিসাম্য রেখা থাকে না। তবে, বিশেষ স্থাপত্যশৈলীর বাড়ির চিত্রে, যেমন উত্তরা গণভবন বা হোয়াইট হাউস, প্রতিসাম্য দেখা যেতে পারে।
খ) একটি মসজিদের চিত্র সমাধান: অধিকাংশ মসজিদের চিত্রে প্রতিসাম্য রেখা বিদ্যমান, যেমন ষাট গম্বুজ মসজিদ ও মুসা খাঁ মসজিদ।
গ) একটি মন্দিরের চিত্র সমাধান: অধিকাংশ মন্দিরের চিত্রে প্রতিসাম্য রেখা দেখা যায়, উদাহরণস্বরূপ ঢাকেশ্বরী মন্দির ও কান্তজির মন্দির।
ঘ) একটি গীর্জার চিত্র সমাধান: অধিকাংশ গীর্জার চিত্রে প্রতিসাম্য রেখা থাকে।
ঙ) একটি প্যাগোডার চিত্র সমাধান: অধিকাংশ প্যাগোডার চিত্রে প্রতিসাম্য রেখা বিদ্যমান।
চ) পার্লামেন্ট ভবনের চিত্র সমাধান: বাংলাদেশ জাতীয় সংসদ ভবনের চিত্রে একটি প্রতিসাম্য রেখা আছে।
ছ) একটি মুখোশের চিত্র সমাধান: অধিকাংশ মুখোশের চিত্রে প্রতিসাম্য রেখা বিদ্যমান।
জ) তাজমহলের চিত্র সমাধান: তাজমহলের চিত্রে একটি প্রতিসাম্য রেখা দেখা যায়।
৬. প্রতিসাম্য রেখা দেওয়া আছে (ড্যাশযুক্ত রেখা), জ্যামিতিক চিত্র সম্পূর্ণ কর এবং শনাক্ত করঃ

সমাধানঃ
প্রতিসাম্য রেখার সাপেক্ষে প্রদত্ত জ্যামিতিক চিত্রগুলো সম্পূর্ণ করে তাদের শনাক্ত করা হলোঃ


সমাধানঃ
প্রদত্ত জ্যামিতিক চিত্রসমূহের প্রতিসাম্য রেখা নীল রেখা দ্বারা নিচের চিত্রে নির্দেশ করা হলোঃ


সমাধানঃ
নিচে অসম্পূর্ণ জ্যামিতিক চিত্রসমূহ সম্পূর্ণ করা হলো (লাল চিহ্ন দ্বারা) যা আয়না রেখা সাপেক্ষে প্রতিসমঃ


জ্যামিতিক প্রতিসমতা
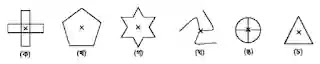
সমাধানঃ
ক) চিত্রে ঘূর্ণন প্রতিসমতা 4
খ) চিত্রে ঘূর্ণন প্রতিসমতা 5
গ) চিত্রে ঘূর্ণন প্রতিসমতা 6
ঘ) চিত্রে ঘূর্ণন প্রতিসমতা 3
ঙ) চিত্রে ঘূর্ণন প্রতিসমতা 4
চ) চিত্রে ঘূর্ণন প্রতিসমতা 3
১০. ইংরেজী বর্ণমালার যে সকল বর্ণেরঃ
ক) অনুভূমিক আয়না
খ) উলম্ব আয়না
গ) আনুভূমিক ও উলম্ব উভয় আয়না
সাপেক্ষে প্রতিফলন প্রতিসমতা রয়েছে সেগুলো আঁক।
সমাধানঃ
ক) ইংরেজি বর্ণমালার যে সকল বর্ণের অনুভুমিক আয়না সাপেক্ষে প্রতিফলন প্রতিসমতা রয়েছে সেগুলো প্রতিসাম্য রেখাসহ (নীল রেখা) আঁকা হলোঃ



১১. প্রতিসমতা নেই এমন তিনটি চিত্র অঙ্কন কর।
সমাধানঃ
প্রতিসমতা নেই এমন তিনটি চিত্র মাছ, পাখি ও বিষমবাহু ত্রিভুজ নিচে আঁকা হলোঃ

১২. একটি লেবু আড়াআড়ি কেটে চিত্রের ন্যায় আকার পাওয়া গেল। সমতলীয় চিত্রটি ঘূর্ণ্ন প্রতিসমতা নির্ণয় কর।

সমাধানঃ
সমতলীয় চিত্রটি ঘূর্ণ্ন প্রতিসমতা চিত্র নিচে আঁকা হলোঃ

ঘূর্ণন প্রতিসমতার মাত্রা=8
১৩. শূন্যস্থান পূরণ করঃ
সমাধানঃ
প্রদত্ত ছকের শূন্যস্থান পূরণ করে নিচে দেওয়া হলোঃ
| চিত্র | ঘূর্ণন কেন্দ্র | ঘূর্ণন প্রতিসমতার মাত্রা | ঘূর্ণন প্রতিসমতার কোণ |
| বর্গ | কর্ণদ্বয়ের ছেদবিন্দু | 4 | 900 |
| আয়ত | কর্ণদ্বয়ের ছেদবিন্দু | 2 | 1800 |
| রম্বস | কর্ণদ্বয়ের ছেদবিন্দু | 2 | 1800 |
| সমবাহু ত্রিভুজ | মধ্যমাত্রয়ের ছেদবিন্দু | 3 | 1200 |
| অর্ধবৃত্ত | কেন্দ্র | 1 | 3600 |
| সুষম পঞ্চভুজ | ভরকেন্দ্র | 5 | 720 |
১৪. যে সকল চতুভুজের রেখা প্রতিসমতা ও 1 এর অধিক মাত্রার ঘূর্ণন প্রতিসমতা রয়েছে, এদের তালিকা কর।
সমাধানঃ
যে সকল চতুর্ভুজের রেখা প্রতিসমতা ও 1 এর অধিক মাত্রার ঘূর্ণন প্রতিসমতা রয়েছে তাদের তালিকা নিচে দেয়া হলোঃ
| চতুর্ভুজ | রেখা প্রতিসমতা | ঘূর্ণন প্রতিসমতার মাত্রা |
| বর্গ | আছে | 4 |
| রমবস | আছে | 2 |
| আয়ত | আছে | 2 |
১৫. 1 এর অধিক মাত্রার ঘূর্ণন প্রতিসমতা রয়েছে এরুপ চিত্রের ঘূর্ণন কোণ 180 হতে পারে কি? তোমার উত্তরের পক্ষে যুক্তি দাও।
সমাধানঃ
1 এর অধিক মাত্রার ঘূর্ণন প্রতিসমতা রয়েছে এরুপ চিত্রের ঘূর্ণন কোণ 180 হতে পারে।
যুক্তিঃ
আমরা লক্ষ করেছি যে,
সমবাহু ত্রিভুজের ঘুর্ণন কোণ 1200=3600/3 এবং ঘূর্ণন প্রতিসমতার মাত্রা 3.
বর্গক্ষেত্রের ঘুর্ণন কোণ 900=3600/4 এবং ঘূর্ণন প্রতিসমতার মাত্রা 4.
সুষম পঞ্চভুজের ঘুর্ণন কোণ 720=3600/5 এবং ঘূর্ণন প্রতিসমতার মাত্রা 5.
তাহলে, 20টি সুষম বাহুবিশিষ্ট বহুভুজের ঘূর্ণন কোণ হবে, 3600/20=180 এবং ঘুর্ণন প্রতিসমতার মাত্রা হবে 20.

















Leave a Comment